Solución problema n·1
Hola a todos los seguidores de este blog. Hoy vamos a mostrar la solución del problema 1.
In primer lugar, quería aclarar algunas definiciones, como:
baricentro o centroide, ortocentro y circuncentro.
Baricentro
En geometría, el centroide o baricentro de un objeto perteneciente a un espacio -dimensional es la intersección de todos los hiperplanos que dividen a en dos partes de igual n-volumen con respecto al hiperplano.
perteneciente a un espacio 
-dimensional es la intersección de todos los hiperplanos que dividen a 
Ortocentro
Se denomina ortocentro (símbolo H) al punto donde se cortan las tres alturas de un triángulo.
El nombre deriva del término griego orto, que quiere decir recto, en referencia al ángulo formado entre las bases y las alturas.
El ortocentro se encuentra en el interior del triángulo si éste es acutángulo; coincide con el vértice del ángulo recto si es rectángulo, y se halla en el exterior del triángulo si es obtusángulo.
Circuncentro
El circuncentro de un triángulo es el punto donde se cortan las mediatrices de los lados. Dicho punto equidista de los vértices y, por lo tanto, es el centro de la circunferencia circunscrita al triángulo.
Ahora podemos resolver nuestro problema.
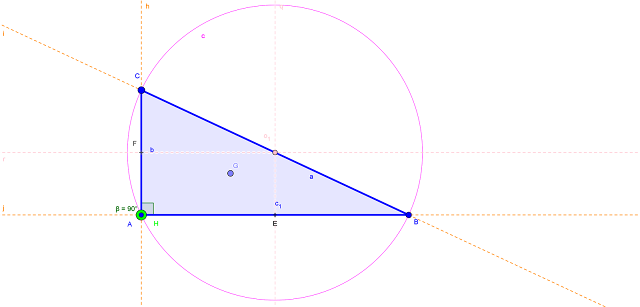
El ortocentro, el baricentro y el circuncentro de un triángulo no equilátero están alineados; es decir, pertenecen a la misma recta, llamada recta de Euler.
Muy interesante entrada, Mariangela, felicidades. Nos muestras las ventajas de la geometría variacional de Geogebra (Juan Alriols estará orgulloso, jaja).
ResponderEliminarComo profe en activo que sufre el déficit de tecnología en las aulas, se me ocurre plantearte: ¿cómo ayudarías a resolver este problema a tus alumnos... sin geogebra, ni reglas, ni compás, ni lápiz siquiera?
Una pista... El papel puede plegarse... es pura geometría ;)
Saludos y ánimo con ese máster.